[2학년][2학기][시스템최적화][2w]
2023. 9. 13. 00:20
1. 메타휴리스틱의 필요성
외판원 문제(Traveling Salesman Problem: TSP)
- Scheduling 혹은 Sequence 문제
- 가장 유명한 조합 최적화 문제
- 여러 도시를 하나의 경로로 이동할 때, 전체 이동 거리가 최소가 되는 경로 찾는 문제
- 각각의 도시를 정확하게 한 번만 방문해야 함
예시
- 원은 도시, 선 위의 숫자는 거리, 도시 1번이 출발지이자 도착지

접근방법
열거법
- 6개의 도시(n-1, 도시 1은 고정)를 순서대로 나열하는 경우의 수는 6! = 720
- 서로 역순인 2개의 경로는 동일한 결과이므로 720/2 = 360 → 절반은 infeasible
- n개의 도시가 있다면 $(n-1)!/2$
- n이 커질수록 지수적으로(exponentially) 증가함 → NP-Complete
- 따라서 최적해를 찾기는 매우 어려움
- Non Polynomial Time(NP) ↔ Polynomial Time
휴리스틱 방법
- 부분 경로 전환(Sub-tour reversal) 알고리즘
- [1-2-3-4-5-6-7-1]에서 부분 경로인 [3-4]를 전환하면 [1-2-4-3-5-6-7-1]이 됨
- 경로 길이는 65가 됨 → 짧은 경로를 찾음(개선됨)
부분 경로 전환 알고리즘(정리)
초기화
- 임의의 가능해를 찾음
반복
- 현재의 해에 대해서 모든 가능한 부분 경로 전환을 고려함
- 가장 많이 개선되는 해를 선택함
- 개선 결과가 동일한 해가 복수 개 있으면 임의로 한 개를 선택함
중지 규칙
- 모든 경우에 대해서 개선이 발생하지 않을 때
- 그 때까지 찾은 가장 좋은 해를 최종해로 선택함
알고리즘 적용 결과
초기화
임의의 경로: [1-2-3-4-5-6-7-1], D = 69
반복1: 부분 경로의 길이는 2~5 가능, 6개를 전환하면 동일한 역순의 경로
- 부분 경로의 길이가 2일 때
- Reverse 2-3: [1-3-2-4-5-6-7-1] D = 68
- Reverse 3-4: [1-2-4-3-5-6-7-1] D = 65
- Reverse 4-5: [1-2-3-5-4-6-7-1] D = 65
- Reverse 5-6: [1-2-3-4-6-5-7-1] D = 66
- 부분 경로의 길이가 3 이상일 때는 전환이 불가능
- Reverse 3-4를 선택함
반복2
- Reverse 3-5-6: [1-2-4-6-5-3-7-1]: D = 64
반복3
- Reverse 3-7: [1-2-4-6-7-3-1]: D = 66
- Reverse 6-5-3: [1-2-4-3-5-6-7-1]: D = 65
- 개선되는 부분 경로 전환 방법이 없음 → 중지
최종해
- [1-2-4-6-5-3-7-1]
- 거리 = 64
- 그러나 이 경로는 최적해가 아님, 더 짧은 경로가 있음
비선형(Non-linear) 함수 최적화 문제(NLP)
함수 f(x)를 최대화 시키는 변수 x를 구하는 문제

접근 방법
- 그래프 그리기: 쉽지 않음
- 계산: f’(x) = 0이 4차식이므로 해를 구하기 쉽지 않음

휴리스틱
- 휴리스틱 1: 기울기 탐색 방법
- 만약 x = 0에서 검색이 시작된다면, 오른쪽으로 x=5까지 움직이고 정지함
- 그러나 그 점은 최적해가 아님
- 휴리스틱 2: 양분법
- 하한 = 0, 상한 = 6으로 해서 검색이 시작된다면, 양분법에 의해서 x = 3, x = 4.5, x = 5.25, x = 4.875 등의 값을 찾으며, 점점 x = 5에 수렴함
- 그러나 그 점은 최적해가 아님
특징
- 이러한 휴리스틱들은 중지조건을 만나면 그대로 종료
- 더 이상 좋은 해를 찾을 수 없기 때문 → 지역 최적해일 가능성 높음
- 단점
- 여러 개의 지역 최적해를 갖는 문제에서는 그 중 하나의 지역 최적해를 찾고 종료될 수 있음
- 휴리스틱의 시작 위치에 따라 찾은 해의 성능이 달라질 수 있음
개선 방법
- 이러한 휴리스틱을 여러번 반복해서 적용 → 대규모 문제에서는 비효율적
- 좀 더 구조적인 접근 방법을 적용 → 메타휴리스틱
2. 유전자 알고리즘
기본 개념
- 19세기 중간 찰스 다윈에 의해 제안된 진화론을 모방
적자 생존의 법칙
- 일반적으로 자식(offspring)은 부모 각각의 염색체 일부를 물려받음 → 교차(crossover)
- 염색체(chromosome) 내의 유전자(gene)는 자식의 특성(feature)을 결정함
- 이때, 부모의 좋은 특성을 물려받은 자식은 더 좋은 특성을 가질 수 있음
- 한편, 자식이 부모 염색체의 유전자에 없는 특성을 무작위(random)하게 가질 수 있음 → 돌연변이(mutation)
- 때로는 돌연변이가 더 좋은 결과로 나타날 수도 있음
알고리즘 설계 개념
- 주어진 문제의 가능해(feasible solution)을 염색체로 표현
- 염색체의 우수성을 목적함수를 이용하여 평가 → 적합도
- 염색체의 교차, 돌연변이 연산으로 새로운 가능해를 찾아감
염색체 설계
- 벡터를 이용하여 표현하며, 문제에 대한 가능해로 해석이 가능해야 함
- TSP 예제의 경우, 벡터 [1,2,3,4,5,6,7,1]은 하나의 경로를 나타냄
- NLP 예제의 경우, 이진수를 이용하여 표현 가능함: 벡터 [1 1 0]은 6을 이진수로 나타냄
- 가능해를 벡터로 표현하는 방법은 문제에 따라 다양할 수 있음
염색체 평가
- 고려하는 문제의 목적함수를 이용하여 평가함
- TSP 예제의 경우, 염색체 [1,2,3,4,5,6,7,1]은 이 순서대로 각 도시를 경유하는 것이므로, 이 경로의 전체 길이는 각 구간에 대한 거리의 합 = 69
- NLP 예제의 경우, 염색체 [1 1 0]은 x = 6을 나타내므로 이를 함수에 대입하면 f(6) = 3,257,712
- 어떤 염색체가 좋은 것인지 판정 가능
유전법칙 - 교차(crossover)
- 부모 염색체를 자손이 물려받는 현상 (확률적으로 발생함, rate of crossover: 0 < rc < 1)
- rc는 보통 크게하여 crossover가 자주 발생하도록 설정
- 2개의 부모가 2개의 자손을 만들어냄
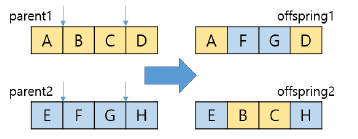
일점교차
- 염색체의 한 점을 임의로 정하고, 그 점을 중심으로 유전자를 교차

이점교차
- 염색체의 두 점을 임의로 정하고, 그 사이에 있는 유전자를 교차
유전법칙 - 돌연변이(mutation)
- 유전자 일부가 바뀌는 현상(확률적으로 발생함, rate of mutation: 0 < rm < 1)
- rm은 보통 작게하여 mutation이 가끔 발생하도록 설정
위치 교환

값 변경

유전자 알고리즘
초기화
- Random하게 초기 염색체를 여러 개 생성 → 크기 N인 초기 모집단 생성
- 각 염색체의 성능을 평가함 → 적합도 평가(염색체들의 우수성 평가 가능)
- 각 연산의 비율 rc와 rm 값을 정함
반복
- 모집단 전체 또는 일부 Q개(짝수)를 선택해서 부모를 만듦
- 6개를 선택한 경우, (1,6),(2,5),(3,4) 또는 (1,2),(3,4),(5,6) 등과 같이 다양하게 부모 쌍 선택 가능
- 각 쌍으로부터 2개씩의 자손을 생성
- 교차 연산과 돌연변이 연산을 적용함: 각각 난수 r을 발생시켜서 r과 rc, rm을 비교하여 연산 적용
- 만일 생성된 자손이 infeasible이면 다시 생성함
- 새로 생성된 자손의 개수 = Q
- 염색체의 중복 발생 가능
- Q개의 자손 염색체에 대한 적합도를 평가함
- 새로운 모집단 생성
- 현재 모집단에 있는 염색체와 새로 생성된 염색체 중에서 우수한 적합도를 갖는(적자생존) N개의 염색체를 선택해서 새로운 모집단으로 정의함
- G1과 G2(Q+Q)개 중에서 우수한 Q개 선택
- 이 중에서 가장 좋은 해를 이전 반복까지 찾은 가장 좋은 해와 비교해서 더 좋은 하나를 현재까지 찾은 가장 좋은 해로 정함
종료 조건
- 다음 중 하나의 종료 조건을 적용 가능
- 고정된 횟수만큼 알고리즘을 반복 적용한 후에
- 고정된 컴퓨터 CPU Time 동안만 알고리즘을 반복 적용한 후에
- 몇 번(k) 반복 적용해도 해가 개선되지 않는 경우
- 현재까지 찾은 가장 좋은 해를 최종해로 선택함
3. 예제 - 외판원 문제
파라미터 세팅
- N = 10, rc = 0.9, rm = 0.05
- 중지조건: 5번 연속해서 현재까지 찾은 가장 좋은 해가 개선되지 않을 때
초기모집단 생성
염색체 생성 방법
- 시작노드1의 다음 목적지는 연결된 노드 중 1개를 random하게 선택함
- 1번에 연결된 노드는 2, 3, 7 → 1/3의 확률로 한 개를 선택
- 만일 2번이 선택되었다면, 다음 노드는 3 또는 4 → 1/2 확률로 선택
- 모든 노드가 선택될 때까지 이 과정을 반복함
- 만일 더 이상 선택할 노드가 없다면(dead end), 처음부터 다시 시작함
- N = 10개의 염색체를 생성할 때까지 반복함
- 모든 염색체의 적합도 평가
- 적합도: 경로 상에 포함된 링크들의 거리 합
- 현재까지 가장 좋은 해 = 적합도 1위 염색체
부모염색체 선택
방법 1
- 높은 적합도를 갖는 4개의 염색체(1위 ~ 4위)와 낮은 적합도를 갖는 2개의 염색체(9위 ~ 10위)를 선택하여 두 개씩 쌍을 만듦 → 3쌍
방법 2
- (1위, 10위), (2위, 9위), … , (5위, 6위) → 5쌍
방법 3
- (1위, 2위), (3위, 4위), … ,(9위, 10위) → 5쌍
교차연산적용 → 자손 생성
일점, 이점교차가 적용되지 못함, 동일 노드가 두 개 생김
부모염색체 예시
- P1: [1,2,3,4,5,6,7,1], P2: [1,2,4,6,5,7,3,1]
- 난수를 생성해서 난수<rc면 교차 연산 적용, 아니면 C1 = P1, C2 = P2
자손은 부모 유전자에 연결된 노드 특성을 이용하여 생성 될 수 있음
- 각 자손은 노드 1에서 시작 → C1: [1-?]
- 노드 1에 연결될 노드 선택
- P1에서 노드 1에 연결된 노드: 2, 7
- P2에서 노드 1에 연결된 노드: 2, 3
- 4개 중에 1개를 random하게 선택: 1-2 50%, 1-3 25%, 1-7 25%
- 1-2가 발생했다면, 자손 C1을 1-2로 시작함
- 다음으로 노드 2에 연결될 노드 선택
- P1은 2-3, P2는 2-4를 가짐
- 1개를 random하게 선택함 → 50% 확률로 2-4가 선택됐다면 C1: [1-2-4]
- 노드 4에 연결될 노드 선택
- P1은 4-3, 4-5, P2는 4-6(P2에서 4-2도 있지만 2가 이미 나옴)
- 1/3 확률로 4-3이 선택됐다면 C1: [1-2-4-3]
- 노드 3에 연결될 노드 선택
- P1은 없음, 그러나 부분 경로 전환이 발생한다면, P1은 3-5를 가지고, P2는 3-7
- : 부모 유전자의 영향을 올리기 위해 Trick으로 부분 경로 전환 발생시킴
- 이러한 과정으로 5-6, 6-7이 선택됐다면 C1: [1-2-4-3-5-6-7-1]
- 오류 발생 가능성
- C1: [1-2-4-3-5] 이후에 5-7이 선택됐다면, 이후에 7-6-1이 불가능한 경로
- → 노드 6에서 dead end
- 따라서 C1 생성을 처음부터 다시 시작
돌연변이연산 적용
방법 1
: 새로운 노드가 연결될 때마다 적용
방법 2
: 자손 염색체를 완성한 후, 임의의 유전자 한 개에 대해 적용
적용방법
- 난수 생성, 난수 <rm이면 연산 적용, 아니면 유지
- 방법 1
- C1: [1-2-4] 이후에 4-3이 선택된 경우, 돌연변이 연산을 적용한다면 4-3을 연결하지 않고 부모에게 없는 연결인 4-7을 연결
- 이런 연결이 2개 이상이면 random하게 1개를 선택
- 방법 2:
- C1: [1-2-4-3-5-6-7-1]에 대해 적용하면, 임의로 유전자 1개를 선택하여 값을 변경함
- 이 경우 값을 변경하면 중복된 도시를 방문하게 되므로 다른 방법이 필요함
- 두 지점을 선택하여 부분 경로 변환 적용
- [4-3-5]가 선택되었다면, C1: [1-2-5-3-4-6-7-1]이 됨
오류 발생 가능성
: 돌연변이 결과가 infeasible이 되면 돌연변이 연산을 다시 적용함
자손 평가
: 새로 생성된 자손들의 적합도 평가
모집단 업데이트
- 새로 생성된 자손과 이전 모집단 중에서 우수한 N개 선택
- 이 중에서 가장 좋은 해를 이전 반복까지 찾은 가장 좋은 해와 비교해서 update
중지 조건 확인
- 중지 조건 만족하면 중지
- 그렇지 않으면, 부모 염색체 선택 단계 수행
유전자 알고리즘의 5가지 설계 요소
- 모집단 크기 N (Population size)
- 부모 염색체 선택 방법 (Selection of parents)
- 교차 연산 방법 (Reproduction, Crossover operator)
- 돌연변이 연산 비율 (Mutation rate)
- 중지 조건 (Stopping rule)
'학사 > 아주대 융시공' 카테고리의 다른 글
| [3학년][1학기][디지털제조입문][1w] (0) | 2024.03.05 |
|---|---|
| [2학년][2학기][작업설계및분석][9w] (1) | 2023.10.31 |
| [2학년][2학기][작업설계및분석][2w] (0) | 2023.09.11 |
| [2학년][2학기][자료구조및알고리즘][2w] (0) | 2023.09.08 |
| [2학년][2학기][시스템최적화][1w] (0) | 2023.09.05 |