[AI] CS231n [2] Linear classification
2024. 5. 4. 12:49
Linear Classification
지난 시간
- 이미지를 여러 카테고리 중 하나로 라벨링
- 가까이 있는 것들의 라벨을 활용하는 kNN Classifier
- 몇 가지 단점
- 모든 학습 데이터를 기억, 저장 → 메모리 공간 비효율적
- 테스트 이미지 분류 시 모든 학습 이미지와 비교 → 계산량과 시간 많이 소요
Overview
- Score Function: 데이터를 클래스 스코어로 매핑
- Loss Function: 예측한 스코어와 실제 라벨과의 차이를 정량화
Parameterized mapping from image to label scores
- D 차원의 벡터인 학습 데이터 N개
- K개의 서로 다른 클래스(카테고리)
Linear Classifier
$$ f(xi,W,b)=Wxi+b $$
- x는 모든 픽셀이 [D x 1] 모양을 갖는 하나의 열 벡터
- W는 [K x D] 차원의 행렬
- b는 [K x 1] 차원의 벡터
- D개의 데이터가 함수로 들어와 K개의 숫자가 출력
- Wx 행렬곱 한 번으로 10개의 서로 다른 분류기를 병렬로 계산하는 효과
- 파라미터 W,b는 우리가 조절 가능
- 올바르게 맞춘 클래스가 틀린 클래스보다 더 높은 스코어를 갖도록 조절
- 학습이 끝나면 학습데이터는 필요없이 Parameter만 남음
- 테스트 분류 시 행렬곱 한 번과 덧셈 한 번만 필요
Interpreting a linear classifier
- 가중치에 따라 스코어 함수는 이미지의 특정 위치에서 특정 색깔을 선호하거나 선호하지 않거나를 구분
Analogy of images as high-dimensional points
- 이미지를 고차원 열벡터로 펼쳤기 때문에 각 이미지를 고차원 공간 상의 하나의 점으로 비유 가능
- [D x 1] 모양의 벡터로 펼쳤다면 D개의 차원 공간 상의 한 점
- 즉시 이해가 되지 않아서 쉬운 비유를 해봄
- 열벡터 [2,3]는 x, y축 (2,3)에 대응 가능
- 열벡터 [1,4,-2]는 x, y, z축 (1,4,-2)에 대응 가능
- 열벡터 [3,0, … , 4]는 x1, x2, … ,xD축 (3,0, … ,4)에 대응 가능
- 이해 됐음
- 각 이미지를 2차원 공간에 표현한다면
- 스코어 값이 0이 되는 선이 있고, 선의 바깥 / 안쪽이 스코어가 양 / 음의 방향으로 선형 증가하는 구역
- W의 각 행이 각각 클래스를 구별하는 분류기
- W의 하나의 행을 바꾸면 해당하는 선이 다른 방향으로 회전
- bias b는 해당 선이 평행이동
- bias가 없다면 xi = 0이 들어왔을 때 파라미터에 상관없이 스코어가 0
- 모든 분류들이 원점을 지나게 됨
Interpretation of linear classifiers as template matching
- parameter W의 각 행은 클래스별 템플릿에 해당
- 이미지의 각 클래스 스코어는 각 템플릿과 이미지의 내적을 통해 비교
- 해당 비교, 계산한 스코어를 기준으로 라벨링
- Linear classifier가 템플릿 매칭을 하고있고 학습을 통해 템플릿이 배워짐
- Nearest Neighbor와 비슷한 것을 하고 있으나 각 클래스마다 이미지 한 장을 사용하는 개념
- Lecture Node의 예시에서 horse 템플릿은 머리가 두 개인 말로 보임
- 왼쪽, 오른쪽을 보는 말의 이미지들이 섞여있음
- car 분류기는 붉은 색을 띄는데, 학습 데이터에 빨간색 자동차가 더 많기 때문으로 보임
Bias trick
- 두 가지 parameter bias와 Weight을 매번 동시에 표현하기 번거로움
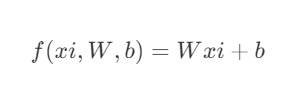
- W의 맨 왼쪽 열에 bias 열을 추가하고, 입력데이터 x의 맨 아래 행에 상수 1로 이루어진 행을 추가
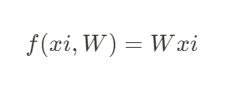
Image data preprocessing
- 입력 데이터를 정규화
- 이미지 전체에 대한 평균 값을 구한 다음 각 이미지에서 이를 빼 이미지의 픽셀이 대략 [-127 ~ 127]의 범위를 가지도록 함
- 입력 데이터(특성)을 스케일링하여 [-1 ~ 1]의 범위를 갖도록 함
Loss Function
- 각 이미지를 틀린 클래스로 분류한 결과에 대한 불만족을 Loss Function으로 측정
- 훈련 데이터의 분류 작업을 잘 수행하지 못하면 높은 Loss를, 잘 수행하면 낮은 Loss를 나타냄
- 이 Loss를 줄이기 위해 가중치를 조절
Multiclass Support Vector Machine Loss Function
- 올바른 클래스 분류의 score가 틀린 클래스 분류의 score보다 margin “Delta” 이상 큰 값을 가지도록 원함
$$ L_i = \sum_{j \neq y_i} \max(0, s_j - s_{y_i} + \Delta) $$
- 올바른 분류의 score가 Delta 만큼 큰 값을 가져야 loss가 0
- 해당 식을 가중치 행렬의 행을 이용한 식으로 변환
$$ L_i = \sum_{j \neq y_i} \max(0, \mathbf{w}_j^T \mathbf{x}i - \mathbf{w}{y_i}^T \mathbf{x}_i + \Delta) $$
Regularization
- 만약 W 행렬이 모든 예시를 정확히 분류한다면 loss는 0
- 이러한 W는 여러개 존재 가능하며, W에 1 이상의 실수를 곱한 가중치 행렬은 모두 loss가 0임
- 가중치가 커지면 학습 데이터에 대한 과적합 우려
- 가중치 행렬에 대한 패널티를 적용하여 가중치가 과도하게 커지는 것을 방지
$$ R(W) = \sum_{k} \sum_{l} W_{k,l}^2 $$
- 가중치 행렬 W의 각 가중치 값들을 제곱한 뒤 더함
- 이를 regularization loss라 하며, 이를 반영한 최종 loss는 아래와 같음
$$ L = \frac{1}{N} \sum_{i} \sum_{j \neq y_i} \left[ \max \left(0, f(\mathbf{x}i; \mathbf{W})j - f(\mathbf{x}i; \mathbf{W}){y_i} + \Delta \right) \right] + \lambda \sum{k} \sum{l} W_{k,l}^2
$$
- 모든 데이터에 대해서 각 이미지의 loss들의 평균과 가중치 행렬의 패널티를 합한, 해당 데이터셋의 최종 multiclass support vector machine loss
- Lambda는 가중치 행렬의 크기를 조절하는 hyperparameter
Practical Considerations
- data loss의 Delta와 regularization loss의 Lambda는 서로 tradeoff
- lambda가 커져 가중치가 커지면 class score간의 차이가 커져 delta값을 넘기기 쉬워짐
- 그렇기 때문에 결국 유일한 조절 변수는 regularization strength인 lambda
Softmax Classifier
- Softmax classifier는 각 class score가 해석 어려운(SVM)값이 아닌 확률로 표현
Summary
- 이미지 픽셀에서 class score를 구하는 score function을 정의
- 이는 가중치 W와 bias b에 의존함
- kNN Classifier와 다르게 학습 데이터는 학습 이후 폐기 가능하며, parameter만 학습하여 새 테스트 이미지에 대해서는 한 번의 행렬곱 연산만 필요함 → Parametric Approach
- bias trick: bias vector를 W 행렬에, x input 데이터에 1 상수 행을 추가하여 bias 열벡터 덧셈 연산을 skip, 편리성 증가
- SVM과 Softmax 두 classifer의 loss function을 define하고 올바른 분류임을 잘 나타내는지를 확인
'Computer Science' 카테고리의 다른 글
| [Paper]You Only Look Once:Unified, Real-Time Object Detection (0) | 2024.08.27 |
|---|---|
| [Paper]ImageNet Classification with Deep Convolutional Neural Networks (0) | 2024.08.09 |
| [AI] CS231n [1] Image Classification (0) | 2024.04.25 |